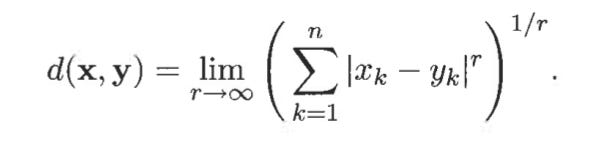Learn Data Science: Similarity Measures and Dissimilarity Measures in Data Science - Part 1
Learn Data Science: Similarity Measures and Dissimilarity Measures in Data Science - Part 1
Video version of the story, if you are into that sort of thing
The term proximity between two objects is a function of the proximity between the corresponding attributes of the two objects. Proximity measures refer to the Measures of Similarity and Dissimilarity. Similarity and Dissimilarity are important because they are used by a number of data mining techniques, such as clustering, nearest neighbour classification, and anomaly detection.
We will start the discussion with high-level definitions and explore how they are related. Then, we move forward to talk about Proximity in two data objects with one simple attribute and moving to objects with multiple attributes.
What is Similarity?
→ It is a numerical measure of the degree to which the two objects are alike.
→ Higher for pair of objects that are more alike.
→ Usually non-negative and between 0 & 1.
0 ~ No Similarity, 1 ~ Complete Similarity
What is Dissimilarity?
→ It is a numerical measure of the degree to which the two objects are different.
→ Lower for pair of objects that are more similar.
→ Range 0 to infinity.
Transformation Function
It is a function used to convert similarity to dissimilarity and vice versa, or to transform a proximity measure to fall into a particular range. For instance:
s’ = (s-min(s)) / max(s)-min(s))
where,
s’ = new transformed proximity measure value,
s = current proximity measure value,
min(s) = minimum of proximity measure values,
max(s) = maximum of proximity measure values
This transformation function is just one example from all the available options out there.
Similarity and Dissimilarity between Simple Attributes
The proximity of objects with a number of attributes is usually defined by combining the proximities of individual attributes, so, we first discuss proximity between objects having a single attribute.
To understand it better, let us go through some examples.
Consider objects described by one nominal attribute. How to compare similarity of two objects like this? Nominal attributes only tell us about the distinctness of objects. Hence, in this case similarity is defined as 1 if attribute values match, and 0 otherwise and oppositely defined would be dissimilarity.
For objects with a single ordinal attribute, the situation is more complicated because information about order needs to be taken into account. Consider an attribute that measures the quality of a product, on the scale {poor, fair, OK, good, wonderful}. We have 3 products P1, P2, & P3 with quality as wonderful, good, & OK respectively. In order to compare ordinal quantities, they are mapped to successive integers. In this case, if the scale is mapped to {0, 1, 2, 3, 4} respectively. Then, dissimilarity(P1, P2) = 4–3 = 1.
For interval or ratio attributes, the natural measure of dissimilarity be- tween two objects is the absolute difference of their values. For example, we might compare our current weight and our weight a year ago by saying “I am ten pounds heavier.”
Moving forward, we are going to talk about Similarity and Dissimilarity between data objects separately. Without further ado, let’s dive into it.
Dissimilarities between Data Objects
We begin with discussion about distances, which dissimilarities with certain properties.
Euclidean Distance
The Euclidean distance, d, between two points, x and y, in one, two, three, or higher- dimensional space, is given by the following formula:
where n is the number of dimensions, and x(k) and y(k) are respectively, the kth attributes (components) of x and y.
Example:
Minkowski Distance
It is the generalisation of Euclidean distance. It is given by the following formula:
where r is a parameter. The following are the three most common examples of Minkowski distances.
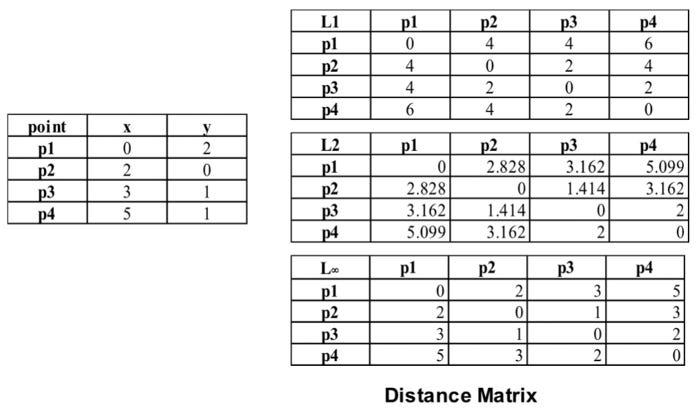
→ r = 1. City block (Manhattan, taxicab, L1 norm) distance. A common example is the Hamming distance, which is the number of bits that are different between two objects that have only binary attributes, i.e., between two binary vectors.
→ r = 2. Euclidean distance(L2 norm).
→ r = infinity. Supremum (L(max), or L(infinity) norm) distance. This is the maximum difference between any attribute of the objects. This is defined by the following formula:
Example:
Distances, such as the Euclidean distance, have some well-known properties. If d(x, y) is the distance between two points, x and y, then the following properties hold.
Positivity
a) d(x, y) > 0 for all x and y,
b) d(x, y) = 0 only if x = y
2. Symmetry
d(x, y) = d(y, x) for all x and y
3. Triangle Inequality
d(x, z) ≤ d(x, y) + d(y, z) for all points x, y and z
The measures that satisfy all three properties are called metrics.